Youve Done It Again Virginia 306

April 9th, 2022 by Roy Due west. Spencer, Ph. D.

SUMMARY

The proper way of looking for causal relationships between time series data (due east.g. between atmospheric CO2 and temperature) is discussed. While statistical analysis lonely is unlikely to provide "proof" of causation, apply of the 'master equation' is shown to avoid mutual pitfalls. Correlation analysis of natural and anthropogenic forcings with year-on-twelvemonth changes in Mauna Loa CO2 advise a role for increasing global temperature at least partially explaining observed changes in CO2, only purely statistical analysis cannot tie down the magnitude. 1 statistically-based model using anthropogenic and natural forcings suggests ~15% of the rise in CO2 being due to natural factors, with an excellent match betwixt model and observations for the COVID-19 related downturn in global economic activity in 2020.

Introduction

The record of atmospheric CO2 concentration at Mauna Loa, Hawaii since 1959 is the longest continuous record we have of actual (not inferred) atmospheric CO2 concentrations. I've visited the laboratory where the measurements are taken and received a tour of the facility and explanation of their procedures.

The geographic location is quite practiced for getting a yearly judge of global CO2 concentrations because it is largely removed from local anthropogenic sources, and at a loftier enough altitude that substantial mixing during air mass transport has occurred, smoothing out sudden changes due to, say, transport downwind of the large emissions sources in China. The measurements are nearly continuous and procedures have been developed to exclude data which is considered to be influenced by local anthropogenic or volcanic processes.

Almost researchers consider the steady rise in Mauna Loa CO2 since 1959 to be entirely due to anthropogenic greenhouse gas emissions, mostly from the burning of fossil fuels. I won't become into the testify for an anthropogenic origin here (e.g. the decrease in atmospheric oxygen, and changes in atmospheric carbon isotopes over time). Instead, I will address bear witness for some portion of the CO2 increase being natural in origin. I will be using empirical information analysis for this. The results will not be definitive; I'one thousand mostly trying to show how difficult it is to determine cause-and-effect from the available statistical data analysis alone.

Inferring Causation from the "Principal Equation"

Many processes in physics tin be addressed with some grade of the "master equation", which is a simple differential equation with the time derivative of one (dependent) variable beingness related to some combination of other (independent) variables that are believed to cause changes in the dependent variable. This equation form is widely used to depict the time rate of change of many physical processes, such as is washed in weather forecast models and climate models.

In the example of the Mauna Loa CO2 data, Fig. one shows the departure between the raw information (Fig. 1a) and the more than physically-relevant twelvemonth-to-year changes in CO2 (Fig. 1b).

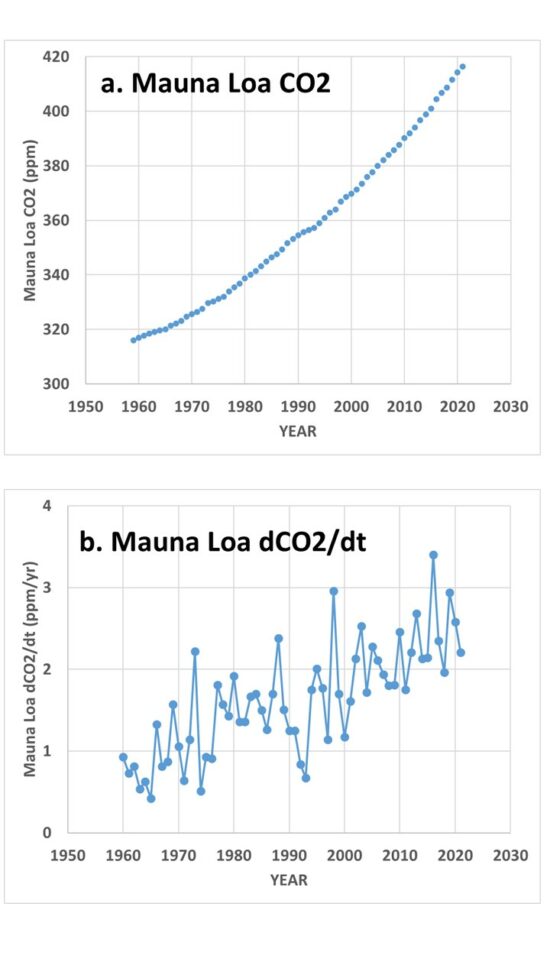
Fig. 1. Mauna Loa CO2 information, 1959-2021, testify equally (a) yearly average values, and (b) twelvemonth-on yr changes in those values (dCO2/dt).

If one believes that yr-to-year changes in atmospheric CO2 are but due to anthropogenic inputs, then we can write:

dCO2/dt ~ Anthro(t),

which simply ways that the year-to-year changes in CO2 (dCO2/dt, Fig. 1b) are a part of (due to) yearly anthropogenic emissions over time (Anthro(t)). In this case, yr-on-yr changes in Mauna Loa CO2 should be highly correlated with yearly estimates of anthropogenic emissions. The actual relationship, notwithstanding, is clearly not that simple, equally seen in Fig. 2, where the anthropogenic emissions curve is much smoother than the Mauna Loa data.

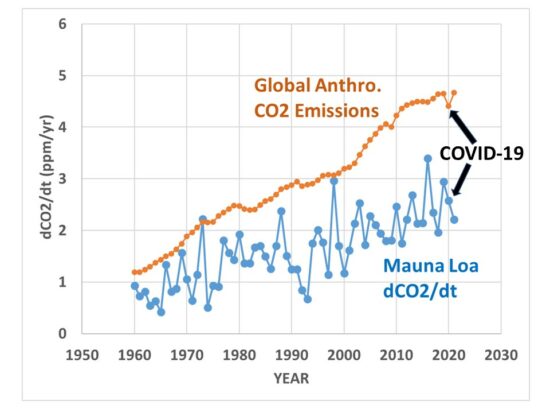
Fig. 2. Mauna Loa twelvemonth-on-year observed changes in CO2 versus estimate of global anthropogenic emissions.

Therefore, there are clearly natural processes at work in addition to the anthropogenic source. Also annotation those natural fluctuations are much bigger than the ~half dozen% reduction in emissions betwixt 2019 and 2020 due to the COVID-19 economical slowdown, a point that was emphasized in a recent study that claimed satellite CO2 observations combined with a global model of CO2 transports was able to identify the small reduction in CO2 emissions.

So, if you think there are also natural causes of year-to-year changes in CO2, yous could write,

dCO2/dt ~ Anthro(t) + Natural(t),

which would approximate what carbon cycle modelers use, since it is known that El Nino and La Nina (every bit well as other natural modes of climate variability) also bear upon yearly changes in CO2 concentrations.

Or, if you think year-on-year changes are due to only sea surface temperature, you can write,

dCO2/dt ~ SST(i),

and you can then correlate yr-on-year changes in CO2 to a dataset of yearly boilerplate SST.

Or, if you call back causation is in the opposite direction, with changes in CO2 causing year-on-year changes in SST, you can write,

dSST/dt ~ CO2(t),

in which case you can correlate the yr-on-year changes in SST with CO2 concentrations.

In addition to the master equation having a basis in physical processes, it avoids the trouble of linear trends in two datasets being mistakenly attributed to a cause-and-effect relationship. Any time serial of data that has but a linear trend is perfectly correlated with every other time serial having just a linear trend, and nonetheless that perfect correlation tells united states of america nix about causation.

Merely when we utilize the time derivative of the data, it is only the fluctuations from a linear tendency that are correlated with another variable, giving some hope of inferring causation. If y'all question that statement, imagine that Mauna Loa CO2 has been ascension at exactly two ppm per twelvemonth, every yr (instead of the variations seen in Fig. 1b). This would produce a linear trend, with no deviations from that trend. But in that example the year-on-year changes are all 2 ppm/year, and since in that location is no variation in those data, they cannot be correlated with anything, because in that location is no variance to exist explained. Thus, using the main equation nosotros avoid inferring crusade-and-effect from linear trends in datasets.

At present, this information manipulation doesn't guarantee we can infer causation, because with a limited set of data (63 years in the example of Mauna Loa CO2 data), yous can await to get some non-zero correlation even when no causal relationship exists. Using the 'master equation' but puts us a step closer to inferring causation.

Correlation of dCO2/dt with Diverse Potential Forcings

Lag correlations of the dCO2/dt information in Fig. 1b with estimates of global anthropogenic CO2 emissions, and with a variety of natural climate indicies, are shown in Fig. three.

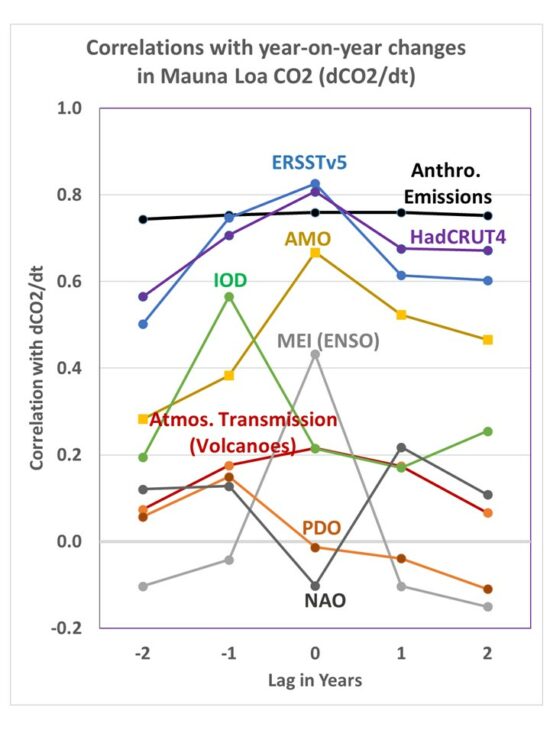
Fig. 3. Lag correlations of Mauna Loa dCO2/dt with various other datasets: Global anthropogenic emissions, tropical body of water surface temperature (ERSST), global average surface temperature (HadCRUT4), the Atlantic Multi-decadal Oscillation (AMO), the Indian Ocean Dipole (IOD), the Multivariate ENSO Index (MEI), Mauna Loa atmospheric transmission (generally major volcanoes),the Pacific Decadal Oscillation (PDO), and the North Atlantic Oscillation (NAO).

The first matter nosotros observe is that the highest correlation is achieved with the surface temperature datasets, (tropical SST or global country+ocean HadCRUT4). This suggests at least some function for increasing surface temperatures causing increasing CO2, specially since if I plow the causation around (correlate dSST/dt with CO2), I get a very low correlation, 0.05.

Next nosotros come across that the yearly estimates of global anthropogenic CO2 emissions is also highly correlated with dCO2/dt. You might wonder, if the IPCC is correct and all of the CO2 increment has been due to anthropogenic emissions, why doesn't it have the highest correlation? The reply could be as unproblematic every bit racket in the information, especially because the emissions estimates from China (the largest emitter) are quite uncertain.

The role of major volcanic eruptions in the Mauna Loa CO2 record is of considerable interest. When the atmospheric transmission of sunlight is reduced from a major volcanic eruption (El Chichon in 1983, and especially Pinatubo in 1991), the effect on atmospheric CO2 is to reduce the rate of rise. This is believed to be the consequence of scattered, diffuse heaven radiation penetrating deeper into vegetation canopies and causing enhanced photosynthesis and thus a reduction in atmospheric CO2.

Regression Models of Mauna Loa CO2

At this point we tin choose whatever forcing terms in Fig. three we want, and exercise a linear regression against dCO2/dt to get a statistical model of the Mauna Loa CO2 record.

For example, if I employ merely the anthropogenic term, the regression model is:

dCO2/dt = 0.491*Anthro(t) + 0.181,

with 57.viii% explained variance.

Permit'southward look at what those regression terms mean. On average, the yearly increase in Mauna Loa CO2 equals 49.1% of total global emissions (in ppm/year) plus a regression constant of 0.181 ppm/yr. If the model was perfect (only global anthropogenic emissions cause the CO2 rise, and we know those yearly emissions exactly, and Mauna Loa CO2 is a perfect approximate of global CO2), the regression abiding of 0.181 would be 0.00. Instead, the anthro emissions estimates practise non perfectly capture the ascension in atmospheric CO2, and then a 0.181 ppm/year "fudge cistron" is in effect included each year by the regression to account for the imperfections in the model. It isn't known how much of the model 'imperfection' is due to missing source terms (east.g. El Nino and La Nina or SST) versus noise in the information.

By using additional terms in the regression, we can become a better fit to the Mauna Loa data. For case, I chose a regression model that includes iv terms, instead of one: Anthro, MEI, IOD, and Mauna Loa atmospheric transmission. In that case I can improve the regression model explained variance from 57.8% to 82.three%. The upshot is shown in Fig. iv.

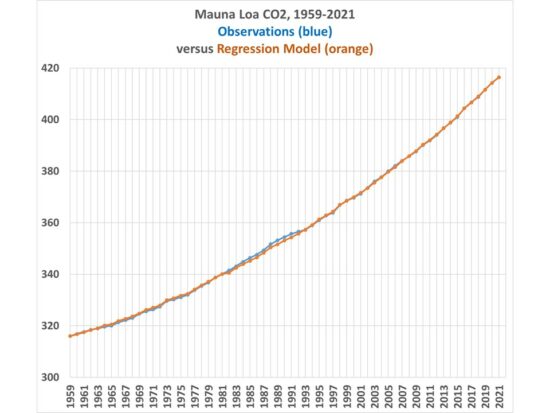
Fig. 4. Yearly Mauna Loa CO2 observations versus a four-term regression model based upon anthropogenic and natural forcing terms.

In this case, the only substantial deviations of the model from observations is due to the El Chichon and Pinatubo volcanoes, since the Pinatubo event caused a much larger reduction in atmospheric CO2 than did El Chichon, despite the volcanoes producing very similar reductions in solar transmission measurements at Mauna Loa.

In this example, the role of anthropogenic emissions is reduced past 15% from the anthro-only regression model. This suggests (but does not prove) a limited part for natural factors contributing to increasing CO2 concentrations.

The model match to observations during the COVID-xix year of 2020 is very close, with only a 0.02 ppm departure between model and observations, compared to the 0.24 ppm estimated reduction in total anthropogenic emissions from 2019 to 2020.

Conclusions

The Mauna Loa CO2 data demand to be converted to twelvemonth-to-year changes earlier being empirically compared to other variables to ferret out possible causal mechanisms. This in event uses the 'chief equation' (a time differential equation) which is the basis of many physically-based treatments of physical systems. Information technology, in event, removes the linear tendency in the dependent variable from the correlation analysis, and trends by themselves have no utility in determining cause-versus-effect from purely statistical analyses.

When the CO2 data are analyzed in this way, the greatest correlations are found with global (or tropical) surface temperature changes and estimated yearly anthropogenic emissions. Curiously, reversing the direction of causation between surface temperature and CO2 (yearly changes in SST [dSST/dt] being caused by increasing CO2) yields a very depression correlation.

Using a regression model that has ane anthropogenic source term and three natural forcing terms, a high level of agreement between model and observations is constitute, including during the COVID-19 year of 2020 when global CO2 emissions were reduced past about 6%.

williamswrinke1952.blogspot.com

Source: https://www.drroyspencer.com/2022/04/explaining-mauna-loa-co2-increases-with-anthropogenic-and-natural-influences/

Share this post